A practical approach to read-write quorum systems

• by Samuele Resca
ℹ️
The 2nd part of this post is available: [Part 2] A practical approach to read-write quorum systems.

Quorum systems allow consistency of replicated data; every time a group of servers needs to agree on something, a quorum is involved in the decisions.

For example, leaderless databases such as Dynamo (not to be confused with DynamoDB) uses a consistency protocol based on quorums[1]. Furthermore, most of the consensus algorithms such as Zab, Raft, Paxos are based on quorums[2].

Read-write quorums define two configurable parameters, R and W.
R is the minimum number of nodes that must participate in a read operation, and W the minimum number of nodes that must participate in a write operation.

A few weeks ago, I came across this tweet:


The tweet refers to the following publication:

Read-Write Quorum Systems Made Practical - Michael Whittaker, Aleksey Charapko, Joseph M. Hellerstein, Heidi Howard, Ion Stoica

The paper reviews some concepts of the quorum systems, and it presents a concrete tool named "Quoracle" that explores the trade-offs of the read-write quorum systems.

Quoracle provides an alternative to the majority quorum systems that are widely adopted in distributed systems. The majority quorum can be defined as

$$ \frac{n}{2} + 1 \space where \space n = n. \space of \space nodes $$

In the case of a read-write quorum systems the majority is represented in a similar way:

$$ r = w = \frac{n}{2} + 1 $$

where \(r\) and \(w\) are the read and write quorums.

Below there are some notes I took while I was reading the paper and a detailed look at the proposed implementation of Quoracle. The topics discussed are listed below:

Quorum system definitions

The paper resumes the definitions and the characteristics of the read-write quorum systems. These concepts are helpful to understand the theory of quorum systems and the implementation of Quoracle.

Given a list of nodes represented as follow:

$$ X = {{x_1,..,x_n}} $$

A read-write quorum system is defined as \(Q = (R, W)\) where \(R\) represents the read quorums, and \(W\) represents the write quorums. \(R\) and \(W\) are sets of subsets of the list of nodes defined in \(X\).

An additional constraint asserts that every read and writes quorum (\(r\) and the \(w\)) must intersect. This is represented with the following definition:

$$ r \in R \space and \space w \in W, r \cap w \neq 0 $$

It is possible to illustrate a quorums systems with a grid as follow:

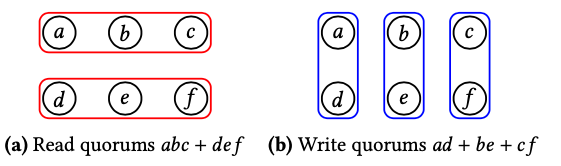
2 by 3 grid quorum system Q2×3

The grid above describes a \( Q_{2x3} \) quorum system defined as \( Q_{2x3} = (abc + def, ab + bc + ac)\).

Note that multiplication represents the nodes that are part of the same set while the addition separates the groups. This approach will be helpful to define read and write sets in Quoracle.

Fault tolerance

The paper describes the read fault tolerance of a quorum system as the largest number, called \(f\), of nodes that can fail before a read quorum is still available. The same definition is applied to the write fault tolerance.

The fault tolerance of a quorum system is the minimum between the read fault tolerance and the write fault tolerance. For example, the \(Q_{2x3}\) quorum system defined above has a read fault tolerance of 1 because if one node is down, it means that only a single read quorum will be available. On the other hand, the write fault tolerance is 2 because if two nodes fail, then there will be only 1 write quorum available.

In this case, the fault tolerance of the quorum system is equal to 1.

Strategy

The paper describes the concept of strategy of a read-write quorum system: the strategy of a quorum system, represented in the paper as \(\sigma\), decides which quorum to contact.

The strategy of a read-write quorum system is represented as:

$$ \sigma = (\sigma_R, \sigma_W) $$

where \(\sigma_R\) and \(\sigma_W\) are probabilities distributions: \(\sigma_R(r)\) and \(\sigma_W(w)\) are respectively the probabilities that the strategy choose a read quorum \(r\) and a write quorum \(w\).

Load, capacity and the read fraction

The read load of a node \(x\), represented as
\(load_{\sigma_R}(x)\) is the probability that the \(\sigma_R(r)\) choose a read quorum \(r\) that contains the node \(x\). The same approach can be taken for the \(load_{\sigma_W}(x)\) .

For calculating the total load of a node \(x\), we need to introduce another parameter: the read fraction.

The read fraction, represented as \(f_r\), is the percentage of reads vs. write operations in a workflow. For example, a workflow with 50% read operations and 50% write operations has a read fraction \( f_r = 0.5 \).

Therefore, the total load of x can be represented by the following definition:
$$ load(x) = f_rload_{\sigma_R}(x) + (1 - f_r)load_{\sigma_W}(x) $$

The load of the quorum system is the load of the optimal strategy, defined as the strategy that brings the lowest load.

The capacity can be repsented as the inverse of the load:

$$ C = \frac{1}{L} \hspace{0.5cm} where \hspace{0.5cm} L = load $$

Higher is the load on the quorums; lower is the capacity of the quorum system.

In conclusion, these are some of the definitions illustrated in the paper. This section gives a good overview of the possible parameters that can influence the performance and the efficiency of read-write quorum systems. The following excerpt is more practical, and it shows the application of these definitions on the implementation of Quoracle.

Quoracle overview

The concepts introduced in the previous section help understand the implementation of the quoracle library described in the paper, available on GitHub: mwhittaker/quoracle.

Note that the quoracle lib is distributed on PyPI, and it can be referred to in a project using the following command:

pip install quoracle

The paper provides an initial example similar to this:

The snippet above declares nodes using the Node class and the corresponding quorum system defined by the QuorumSystem class. The Node class is used to describe the nodes that are part of the \(X\) set:

Each Node instance has a name, a read_capacity, a write_capacity, and a latency attribute.

The read_capacity, write_capacity and latency attributes represent heterogeneous nodes.

When a read/write capacity is specified for a node, it is used to normalise the node load during the linear optimisation; we will go through the detailed process later in this post.

By default, the latency of a Node is 1s. The attribute is used in the linear optimisation process for calculating the latency of the quorum systems.

The multiplication(*) and sum operation(+) are defined by the Expr class that is extended by the Node class:

Each Node instance extends the Expr type, this approach allows to compose expressions of nodes, such as the following quorum definition:

  a, b, c = Node('a'), Node('b'), Node('c')
  q = QuorumSystem(reads=a * b + b * c + a * c)

Another key component is the QuourmSystem class: it encapsulates the read and write quorums of the system, and it defines some methods for calculating the optimal strategy: the load, the latency, and the network load.

The snippet below defines the QuorumSystem class implemented by the library and the signature of the key methods exposed by the class:

The snippet above defines four methods for the class QuorumSystem: load, capacity, network_load, latency. We will have a detailed look at the implementation of the methods later in this section. First, however, all these methods have a similar signature: they require an optimize parameter representing the objective of the optimisation, either the read_fraction or the write_fraction parameters (already described in the theory section), and some additional constraints used by the optimisation of the quorum strategy, such as the load_limit, network_limit, latency_limit parameters.

As you may have noticed, the initialisation of the quorum system only provides the following read quorums:

ab + bc + ac

In this case, the library will derive the optimal write quorums by applying a dual operation to the given quorum. For example, the result of the dual process on the ab + bc + ac quorum calculates:

(a + b) * (b + c) * (a + c)

Once the QuorumSystem is initialised, it is possible to calculate the load, the latency, and the network_load of the system.

Optimal strategy problem implementation

This section dig into the optimal strategy implementation. The load, capacity, network_load and latency methods in the QuorumSystem class use the concept of optimal strategy, referred in the paper as \( \sigma^{\ast} = (\sigma_R^{\ast}, \sigma_W^{\ast}) \).

A strategy can be optimal in respect of the load, the network, or the latency. The objective of the optimisation can be configured using the optimize parameter.

The internal implementation turns the optimisation into a linear programming problem, and it relies on PuLP to find the optimal strategy.

In the following sections, we discover the different optimisation objectives provided by Quoracle.

Load optimization

In case the optimize == LOAD then the objective of the linear optimiation is the load. The implementation of the load optimization works as follow:

The implementation minimizes the load using the following definition:

$$ \frac{f_r}{cap_R(x)} \sum_{{r \in R | x \in r }} p_r +  \frac{1 - f_r}{cap_W(x)}  \sum_{{w \in W | x \in w }}  p_w \leq L_{f_r} $$

For each read_fraction (\(f_r\)) in the QuorumSystem, the load method proceeds by computing the load by calling fr_load method.

As a first step, the fr_load method defines the \(L_{f_r}\) variable, representing the load for that read fraction.
It continues by adding the read quorum part of the definition above:

x_load += fr * sum(vs) / self.node(x).read_capacity

the same for the write quorum part:

x_load += (1 - fr) * sum(vs) / self.node(x).write_capacity

As a final step, it proceeds by finalising the constraint using the instruction:

problem += (x_load <= l, f'{x}{fr}')

Network load optimization

The following expression defines the network load.

$$ f_r ( \sum_{r \in R} p_r  \cdot |r|) + (1 - f_r) ( \sum_{w \in W} p_w  \cdot |w|) $$

Where \(|r|\) and \(|w|\) are the length of the read and write quorums sets.

In concrete, the library implements the following code:

If optimise == NETWORK, quoracle will use the network function above as a target objective for the optimal strategy. The implementation follows the network load definition mentioned above. Each read and write quorum multiplies the quorum length with the read_quorum_vars and write_quorum_vars, and it sums the values together.

If \(f_r\) is a distribution, the network load is computed as a weighted average of all the network loads derived by every single value in the distribution.

Latency optimization

The latency is another important aspect of a quorum system. In the real world, nodes are heterogeneous, and the latency depends on the network conditions and the status of the node that we are contacting.

The paper defines the latency as:

$$ f_r ( \sum_{r \in R} p_r \cdot latency(r)) + (1 - f_r) ( \sum_{w \in W} p_w \cdot latency(w)) $$

In practice, in case optimize == LATENCY, Quoracle uses the following approach for calculating the latency:

The Node class has a configurable latency. The implementation builds the latency minimisation problem by multiplying the latency in seconds assigned to each node with the read and write quorums. If \(f_r\) represents a distribution, then the implementation uses the weighted average of the values in the distribution to get the final result.

Additional constraints

As we saw previously, the target of linear optimisation depends on the optimize parameter. Therefore, the resulting optimal strategy will be optimal regarding the load, the network load, or the latency.

In addition, it is possible to specify some additional constraints for the optimal strategy: these constraints are limits on the load, the network, or the latency.

Note that it is not possible to optimise for load and at the same time specify a load limit to the strategy; the same restriction is valid for the network and the latency.

The additional constraints use the same definitions of load, network latency, and latency we saw previously. This example shows a final problem that defines an optimal load strategy with some constraints on the network and the latency.

Let's take for example the following optimization query:

q = QuorumSystem(reads=a * b + b * c + a * c)

q.load(optimize=LOAD, read_fraction=1, network_limit=3, latency_limit=datetime.timedelta(seconds=2))

The QuorumSystem is defined by some quorums composed of three nodes: a, b, c. We want to get the optimal load (optimize==LOAD), with a read_fraction of 1 (100% reads workflow), a network_limit==3 and a latency of 3 seconds (by default, every Node has a latency of 1s if we not specify anything.). The resulting optimisation problem that finds the optimal strategy looks like this:

optimal_strategy:
    MINIMIZE
        1.0*l_1.0 + 0.0
    SUBJECT TO
        valid_read_strategy: r0 + r1 + r2 = 1
        valid_write_strategy: w0 + w1 + w2 + w3 + w4 + w5 + w6 + w7 = 1
        a1.0: - l_1.0 + r0 + r2 <= 0
        b1.0: - l_1.0 + r0 + r1 <= 0
        c1.0: - l_1.0 + r1 + r2 <= 0
        network_limit: 2 r0 + 2 r1 + 2 r2 <= 3
        latency_limit: r0 + r1 + r2 <= 2

As you can see, the optimal strategy problem tries to minimise the load in respect of some constraints:

  • valid read/write strategies: the sum of all the read/write probabilities is 1;
  • the a1.0, b1.0, c1.0 are the constraints which represent the load optimization. In detail, the constraint a1.0 representing the load for node a, use the constraint r0 + r2 <= l_1.0;
  • the network_limit must be less than three as we specified in the load method call above;
  • the latency_limit must be less than 2s as we specified in the load method call above;

The reference to the optimal_strategy problem is then optimised, and the resulting values, encapsulated in a pulp.LpVariable instance, are passed to a new Strategy type.

Strategy representation

Quoracle uses a Strategy class to represent the concept of strategy (σ) for the quorum system. The following snippet of code describes the implementation and the constructor of a Strategy[T] type:

The class extends a Generic[T] type, and it wraps a reference to a QuorumSystem[T] type, a sigma_r, and a sigma_w attribute, the last two properties represents the definition of strategy we saw in the first section:

$$ \sigma = (\sigma_R, \sigma_W) \newline$$

The Strategy constructor initializes two dictionaries: the x_read_probability and x_write_probability. They provide a map between node x and its probability of getting selected as part of a quorum.

The Strategy class exposes the methods for retrieving the read and write quorums and the nodes that are part of the quorum systems:

The get_read_quorum and the get_write_quorum methods pick the read/write set depending on the probability of getting selected.

Finally, the Strategy class implements the methods for calculating key characteristics we discussed previously, such as: the load, the capacity, the network_latency, and the latency:

The implementation works similarly to the constraints definitions that define the optimal strategy problem we discussed in the previous sections. Again, it is possible to pass the read_fraction and the write_fraction distributions to represent heterogeneous workflows.

Handling quorum failures

In distributed systems, failures are frequent. The two main approaches adopted in quorum systems are:

  • contact every node in the quorum system in case some of them are failing;
  • contact the minimum amount of nodes and eventually retry if a node fails (retry means losing a significant amount of time);

The paper defines a dynamic value representing a quorum system's resilience, called f-resilience.

\(f\) represents the number of failures that are tolerated by a strategy.

Quoracle capabilities computes the read and write quorums that are f-resilient using DP. The logic is defined in the _f_resilient_quorums method:

Given a \(f\) coefficient, a set of nodes, and expression (Expr) indicating the read and write quorums, the method returns the sets of f-resilient quorums by iterating over all the possible combinations of nodes that can form a valid f-resilient quorum. Note that it is impossible to build resilient quorums in some scenarios: for example, in case f > len(xs). Therefore, the method will return an empty set.

The concept of resilience, as described in the paper, comes with the cost of capacity.

Quoarcle provides a way to search for an optimal quorum depending on a given set of parameters:

def search(nodes: List[Node[T]],
           read_fraction: Optional[Distribution] = None,
           write_fraction: Optional[Distribution] = None,
           optimize: str = LOAD,
           resilience: int = 0,
           load_limit: Optional[float] = None,
           network_limit: Optional[float] = None,
           latency_limit: Optional[datetime.timedelta] = None,
           f: int = 0,
           timeout: datetime.timedelta = datetime.timedelta(seconds=0)) \
           -> Tuple[QuorumSystem[T], Strategy[T]]:
           
           #...

The nodes parameter represents the nodes you have in the quorum system. As already discussed, the read_fraction could be a single value or a Distribution of percentages. Finally, the optimize parameter defines the objective of the optimisation.

The load_limit, network_limit, latency_limit are the additional constraints already explained in the Optimal strategy problem implementation section.

The underlying implementation of the search function uses the types we already described, such as the Strategy and theQuorumSystem classes:

Given a set of nodes, the implementation calculates the list of all the de-duplicated expressions that can be composed with that set of nodes using the _dup_free_exprs function.

The implementation proceeds by calling the do_search function; it initialises a new instance of a QuorumSystem for each previously computed expression.

Once the QuorumSystem is initialised, it proceeds by calling the strategy method to get the optimal strategy for the current expression. If the target parameter for that strategy is more optimal than the previous strategy, it is promoted to an optimal strategy. Otherwise, the algorithm continues.

In terms of interactions, the do_search applies linear programming optimisation for each expression derived from the _dup_free_exprs. However, the computation is time-consuming: the search function accepts a timeout parameter limiting the search's computation time. The implementation checks if the timeout has hit during every iteration in case it stops the computation.

Final thoughts

This post went through the concepts of quorum systems illustrated in the Read-Write Quorum Systems Made Practical - Michael Whittaker, Aleksey Charapko, Joseph M. Hellerstein, Heidi Howard, Ion Stoica paper, and it gave a detailed look at the Quoracle implementation. Quoracle is an excellent foundation to explore the thread-offs of the read-write quorums systems. A closer look at Quoracle implementation helps to understand the critical aspect of implementing quorums in distributed systems.

In the next couple of months, I will implement a Golang port of Quoracle for learning purposes. The port is in progress at the following: samueleresca/quoracle-go. I will probably write a more detailed post that gives a closer look at the Golang implementation.

Below there are the references used to write this post.

References

[1]Dynamo: Amazon’s Highly Available Key-value Store

[2]ZooKeeper: Wait-free coordination for Internet-scale systems

[3]Quorums - Martin fowler

[4]Read-Write Quorum Systems Made Practical - Michael Whittaker, Aleksey Charapko, Joseph M. Hellerstein, Heidi Howard, Ion Stoica