Detecting node failures and the Phi accrual failure detector
Partial failure is an aspect of distributed systems; the asynchronous nature of the processes and the network infrastructure makes fault detection a complex topic.
Failure detectors usually provide a way to identify and handle failures using a constant timeout: after a certain threshold, the failure detector declares the node offline.
This post is the result of some readings and notes related to an alternative approach for failure detection called "φ accrual failure detector".
Most of the concepts are from the following paper:
The φ Accrual Failure Detector - Naohiro Hayashibara, Xavier Défago, Rami Yared and Takuya Katayama
A common way to detect node failures in asynchronous distributed systems is to use a heartbeat signal: let's suppose that we have a p process that pings a q monitor process. If q doesn't receive a heartbeat request from p after a certain delay (Δt), then q can declare p failed.
How long should the timeout be before declaring p offline?
Since we have a binary signal, it is hard to distinguish an offline process from a slow one; we can end up with two different cases:
- A short timeout means that we can potentially declare the node offline even if it is not (aggressive approach), but we will detect offline nodes faster;
- A long timeout reduces the risk of wrongly declaring nodes offline with the cons that the detection will be slower;
Therefore, the timeout value is usually configured with an experimental approach and adjusted manually.
In addition to the process slowness, some additional variables play an important role in a heartbeat timeframe: the network unbounded delays. Different parts of the network infrastructure can slow down the communication between two nodes, such as the TCP retry mechanism or network congestion in a network switch.
An accrual failure detector calculates the variability of the response times based on a sample window, and it provides a dynamic way to identify a dependency failure.
Failure detector architecture
The paper describes the failure detectors with the following components:
- the Monitoring component receives the heartbeat from the network;
- the Interpretation component defines the criteria that establish if a node should be considered available or not;
- the Action component implements the decisions of what to do in case the node is not available based on the outcome of the interpretation component;
The image shows the different parts of a failure detector system.
The left schema represents a standard failure detector: the monitoring and the interpretation phases are implemented within the failure detection system. In this case, the failure detector returns a suspicion flag represented by a boolean value. The application logic does not perform any additional analysis on the value; it proceeds by executing an action depending on the suspicion result.
The schema on the right describes the anatomy of an accrual failure detector. The difference is that the accrual failure detector layer returns a level of suspicious, described by a dynamic numeric value. In this case, both the interpretation and the action are delegated to the application layer. This approach gives the application the freedom to perform different actions depending on the suspicon level and eventually prioritize the job reallocation using the level returned by the accrual failure detector.
φ implementation
The paper proposes an implementation of the accrual failure detector called "The φ accrual failure detector".
The φ is a value that is continuously adjusted depending on the current network conditions.
The heartbeat signals arrive from the network, and each heartbeat interval is stored in a sample window collection which has a fixed size. The sample window collection is used to estimate the distribution of the signals.
The φ value is defined as follow:
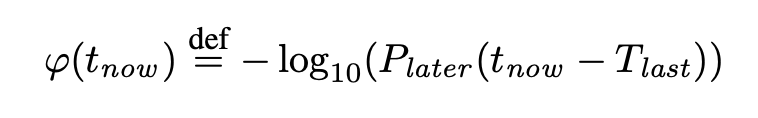
Tlast is when the failure detector received the most recent heartbeat. tnow is the current timestamp. Plater is the probability that a heartbeat will arrive within an interval of time tnow - Tlast.
Since we are storing all the incoming intervals (tnow - Tlast) in the sample window collection, then Plater is calculated using the cumulative distribution function.
Python implementation
The φ accrual failure detector concepts described in the paper are already implemented in akka/akka, and a slightly modified version is implemented in Cassandra.
In this section, I'm describing a python port of the akka implementation. The source is available at the following repo: samueleresca/phi-accrual-failure-detector.
The code implements a φ accrual failure detector class called PhiAccrualFailureDetector.
Note that the implementation focuses on a single instance of the failure detector. Therefore, it ignores some components that are needed for handling multiple instances, such as a failure detector registry (see: akka.remote.DefaultFailureDetectorRegistry).
Sampling window
The implementation of the sampling window collection is in the HeartbeatHistory class:
The HeartbeatHistory class defines a list of intervals and a max_sample_size attribute, which indicates the sampling window size. The class implements some methods that retrieve the mean, the std_dev, and the variance of the distribution.
HeartbeatHistory overrides the sum operation by explicitly declaring the __add__ definition. The method allows adding a new interval to the intervals collection.
In case the size of the intervals exceeds the max_sample_size defined for the collection, the implementation proceeds by removing the oldest value in the list (see the drop_oldest method). This would guarantee the fixed size of the collection.
The _HearbeatHistory class is encapsulated by a _State class:
The _State class represents the accrual failure detector state, and it stores the heartbeat history and the latest heartbeat timestamp (Tlast). The class instance will be wrapped into an AtomicReference to guarantee the thread-safety.
Heartbeat method
The heartbeat method handles the incoming signal from the network. The implementation is described here:
The code above omits some components of the class and focuses only on the heartbeat method.
The implementation uses the get_time() function to retrieve the current time in ms. The get_time() function is also useful to mock the current time in a testing phase.
In case the current state is not defined, it initializes the state with the first heartbeat, represented by the first_heartbeat_estimate_ms attribute.
It proceeds by calculating the interval between tnow - Tlast and stores the interval in the heartbeat history state.
The state is wrapped into an AtomicReference type to handle the cases of multiple threads trying to access the attribute concurrently. The implementation calls the compare_and_set method for comparing the old state with the expected one. If the states do not match, the method retries recursively by calling itself.
Calculating the Phi value
The phi method calculates and returns the actual value of φ computed using the HeartbeatHistory instance encapsulated in the state attribute:
The core of the implementation is defined in the self.calc_phi function. Given the time_diff, the mean, and the std_dev of the distribution, the function computes the logistic approximation of the cumulative normal distribution (for the details, see "A logistic approximation to the cumulative normal distribution" at the bottom of the post). Once the phi value is calculated, it is returned to the caller.
The self.calc_phi function wraps the math.exp operation with a try-except block. If the operation reaches the digits limit and raises an OverflowError exception, it assigns a float(inf) value to e. In case the argument of the math.exp operation is a very large negative value, the result will be rounded to 0.
Another aspect to notice is the different calculations made depending on the timeDiff > mean condition. This is because of a floating-point loss precision concern well-described in the Akka original issue: akka/issues/1821.
Usage example
The following code describes a simple usage of the PhiAccrualFailureDetector class. It mocks the timings by overriding the _get_time() method defined in the class:
The test above defines an Iterable of mocked times as follow:
t0 = 0
t1 = 1000
t2 = 1100
t3 = 1200
t4 = 5200
t5 = 8200
And it executes a sequence of heartbeat methods, which will populate the heartbeat_history state of the accrual failure detector instance. When the test code calls the is_available method for the first time, the value of φ is:
φ: 0.025714293568000528
This is less than the threshold we defined in the class initialization; therefore, is_available will return True. When we call the is_available method for the second time (after skipping the 5200 time), we have a Δt = t5 - t3 = 8200 - 1200 = 7000, which will lead to the following value of φ :
φ: 109.21058212993705
Therefore, the second is_available call returns False since the threshold will be greater than threshold=3 we defined in the initialization.
Conclusion
This post goes through some concepts of the ϕ Accrual failure detector paper, and it describes a concrete python implementation available at the following link: phi-accrual-failure-detector. The code is using a fixed value (phi_value < threshold) to decide if a node/process is available or not. Still, the resulting φ value is dynamic, and the implementation can eventually consider assigning different values of availability depending on the resulting φ value.
Below there are the references I used to write this post.
References
The ϕ Accrual Failure Detector - Naohiro Hayashibara, Xavier Défago, Rami Yared and Takuya Katayama
Phi Accrual Failure Detector - Akka documentation
Cassandra - A Decentralized Structured Storage System
A logistic approximation to the cumulative normal distribution
